решебники и ГДЗ
гдз - готовые домашние задания




Зубарева И.И. Мордкович А.Г.
гдз решебник математика 6 класс
учебник ответы готовые домашние задания
УСЛОВИЕ ЗАДАНИЯ № 853
РЕШЕНИЕ ЗАДАНИЯ № 853
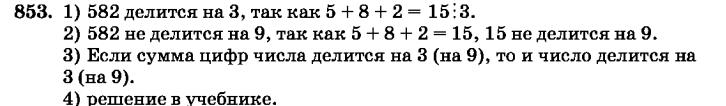
OCR перевод условия задачи № 853
учебника Зубаревой и Мордковича по математике 6 класса
|
853. 1) Не выполняя вычислений, докажите, что число 582 делится на 3.
2) Не выполняя вычислений, определите, делится ли число 582 на 9. 3) Постарайтесь сформулировать признаки делимости на 3 и на 9. 4) Попробуйте доказать признак делимости на 9 для любого трехзначного числа. В случае затруднений прочитайте подсказку: представьте трехзначное число, где а — цифра сотен, Ъ — цифра десятков и с — цифра единиц, в виде суммы разрядных слагаемых и постарайтесь изменить полученное выражение так, чтобы некоторые слагаемые делились на 9. Для того чтобы обосновать признак делимости на 9, запишем трехзначное число в виде 100а + 10Ь + с, где а — цифра сотен, b — цифра десятков и с — цифра единиц этого числа. Тогда: 100а + 10Ь + с = 99а + а + 9Ь + Ь + с = 99а + 9 b + {а + b + с). Подумайте, справедлив ли этот признак для любого натурального Постарайтесь, рассуждая таким же образом, обосновать признак делимости на 3. если сумма цифр числа делится на 3, то и само число делится на 3; если сумма цифр числа делится на 9, то и само число делится ! на 9. Если же сумма цифр числа не делится на 3, то и само число не делится на 3. Поэтому признак делимости числа на 3 обычно формулируют так: натуральное число делится на 3 тогда и только тогда, когда ' делится на 3 сумма его цифр. А признак делимости числа на 9 звучит так: натуральное число делится на 9 тогда и только тогда, когда ! делится на 9 сумма его цифр. |
Как снять комнату в коммунальной квартире здесь
Дренажная система водоотвода вокруг фундамента - stroidom-shop.ru






